Word problems involving systems of linear equations translate real-world scenarios into mathematical models‚ requiring critical thinking and problem-solving skills to identify variables and formulate equations accurately․
Definition and Importance
A system of linear equations consists of multiple equations with the same variables‚ allowing us to solve for unknowns that satisfy all equations simultaneously․ These systems are fundamental in modeling real-world problems‚ such as budgeting‚ resource allocation‚ and engineering designs․ Mastering them enhances analytical and problem-solving skills‚ crucial for STEM fields and everyday decision-making․ They can be represented algebraically‚ graphically‚ or through matrices‚ making them versatile tools for understanding complex relationships․ Solving these systems builds logical thinking and mathematical proficiency‚ essential for tackling practical challenges effectively․
Learning Objectives
By studying systems of linear equations word problems‚ learners will gain the ability to translate real-world scenarios into mathematical equations․ They will master identifying variables‚ setting up equations‚ and solving systems using substitution‚ elimination‚ matrices‚ and graphical methods․ Students will develop problem-solving skills to interpret results in practical contexts‚ ensuring solutions are logical and applicable․ This module aims to enhance critical thinking‚ algebraic manipulation‚ and the ability to verify solutions for accuracy․ Ultimately‚ learners will confidently apply these concepts to diverse fields‚ fostering a deep understanding of linear systems and their everyday applications․

Understanding the Basics of Linear Equations
Linear equations are fundamental in algebra‚ represented as ax + by = c‚ where a and b are coefficients‚ and c is a constant․ They graph as straight lines‚ forming the basis for solving systems of equations and real-world problems․
What Are Linear Equations?
A linear equation is a mathematical expression of the form ax + by = c‚ where a and b are coefficients‚ and c is a constant․ Linear equations represent straight lines when graphed‚ with a constant slope․ They involve variables of the first degree‚ meaning no variable is squared‚ cubed‚ or under a root․ Linear equations can have one or more variables‚ but in systems‚ they typically involve two variables‚ such as x and y․ These equations are foundational for solving systems of equations and modeling real-world problems‚ such as budgeting‚ engineering‚ and economics․ Understanding linear equations is essential for translating word problems into algebraic forms and solving them effectively using methods like substitution or elimination․ They are the building blocks for more complex mathematical models and systems;
Key Concepts: Variables‚ Coefficients‚ and Constants
In linear equations‚ variables are letters that represent unknown values‚ while coefficients are numbers that multiply these variables․ A constant is a numerical value without any variable․ For example‚ in the equation 2x + 3 = 7‚ x is the variable‚ 2 and 3 are coefficients‚ and 7 is the constant․ These elements work together to form equations that can be solved individually or as part of a system․ Understanding these components is crucial for translating word problems into algebraic expressions and solving them effectively․ They form the foundation of linear systems and their applications in real-world scenarios․
Graphical Representation of Linear Equations
A linear equation can be graphed as a straight line on a coordinate plane․ The equation y = mx + b represents a line with slope m and y-intercept b․ When solving systems of linear equations graphically‚ each equation is plotted‚ and the intersection point represents the solution․ This visual method helps in understanding the relationship between variables and verifying solutions․ Graphical representation is particularly useful for identifying parallel lines (no solution) or coinciding lines (infinite solutions)․ It provides a clear‚ intuitive way to analyze and solve linear systems‚ making abstract concepts more tangible for learners․
Translating Word Problems into Algebraic Expressions
Translating word problems involves identifying variables‚ assigning values‚ and converting English sentences into mathematical equations‚ ensuring accuracy in representation and avoiding common pitfalls like misinterpreting terms or operations․
Identifying Variables and Assigning Values
Identifying variables involves pinpointing unknowns in a word problem and assigning them symbols‚ such as x or y․ Assigning values requires translating quantities into numerical or algebraic expressions․ This step ensures clarity and sets the foundation for formulating equations․ Proper identification prevents misinterpretation‚ while accurate assignments maintain problem integrity․ For instance‚ in a mixture problem‚ variables might represent quantities of substances‚ and their values are derived from the problem’s context․ This process is crucial for creating a solvable system of linear equations․
Converting English Sentences into Mathematical Equations
Converting English sentences into mathematical equations involves translating words into algebraic expressions․ Key terms like “more than‚” “less than‚” or “sum of” indicate operations or equality․ Verbs such as “is‚” “will be‚” or “equals” signal assignment or equality․ For example‚ “The total cost is $50” becomes 50․ Prepositions like “of” denote multiplication‚ while “per” suggests division․ This step requires careful interpretation to ensure equations accurately reflect the problem’s intent․ Proper translation is vital for setting up solvable systems of linear equations and achieving correct solutions․
Common Pitfalls in Translation
Common pitfalls in translating word problems into equations include misinterpreting terms like “more than” or “less than‚” which can reverse the equation’s direction․ Forgetting to assign variables correctly or misunderstanding the relationships between quantities can lead to incorrect equations․ Another mistake is misplacing coefficients or constants‚ altering the equation’s meaning․ Additionally‚ assumptions about implicit relationships in the problem can skew the system․ Careful reading and systematic variable assignment help mitigate these errors‚ ensuring accurate translation and solvable systems of equations․

Setting Up Systems of Linear Equations
Setting up systems involves identifying variables and creating equations based on the problem statement‚ ensuring each equation accurately represents the relationships described in the scenario․
Defining Variables Based on the Problem Statement
Defining variables is the first step in translating word problems into algebraic expressions․ Variables represent unknowns‚ such as quantities or values‚ that are crucial to solving the problem․ By carefully analyzing the problem statement‚ you can identify what needs to be found and assign variables accordingly․ For example‚ in a business scenario‚ variables might represent costs or profits‚ while in a mixture problem‚ they could represent quantities of different substances․ Assigning meaningful names or labels to variables helps maintain clarity and ensures that the resulting equations accurately reflect the problem’s context․ This step lays the foundation for formulating the system of equations needed to find the solution․
Formulating Equations from Word Problems
Formulating equations from word problems involves translating descriptive sentences into mathematical expressions․ This requires identifying key information such as relationships between variables‚ constants‚ and coefficients․ For instance‚ phrases like “twice as many” or “sum of” indicate specific operations or combinations․ By breaking down the problem into simpler parts and assigning variables‚ you can construct equations that represent the scenario․ Ensuring that each equation accurately reflects the problem’s conditions is crucial for setting up a solvable system․ Practice and attention to detail are essential to master this skill‚ as it forms the core of solving systems of linear equations․
Ensuring Consistency in the System
Ensuring consistency in a system of linear equations involves verifying that all equations align with the problem’s conditions and that variables are defined uniformly․ This includes checking that units‚ terms‚ and relationships are logically coherent across all equations․ Each equation must accurately reflect the problem’s context without introducing contradictions․ Practical steps include reviewing variable assignments‚ ensuring dimensional consistency‚ and validating that each equation logically follows from the problem statement․ Consistency is critical for accurately solving the system and deriving meaningful solutions that align with real-world scenarios․ Attention to detail and thorough review are essential to maintaining a reliable system․

Solving Systems of Linear Equations
Solving systems of linear equations involves methods like substitution‚ elimination‚ or matrix operations to find variable values that satisfy all equations simultaneously․
Substitution Method: Step-by-Step Explanation
The substitution method involves solving one equation for a variable and substituting this expression into the other equation․ Step 1: Solve one equation for a variable․ Step 2: Substitute this expression into the second equation․ Step 3: Solve the resulting equation for the remaining variable․ Step 4: Substitute this value back into the original expression to find the first variable․ This method is effective for systems with one equation easily solvable for a variable‚ ensuring accurate solutions through systematic substitution and back-replacement․
Elimination Method: Step-by-Step Explanation
The elimination method solves systems of linear equations by eliminating one variable to find the other․ Step 1: Multiply equations to align coefficients of one variable․ Step 2: Subtract or add equations to eliminate the variable․ Step 3: Solve for the remaining variable․ Step 4: Substitute this value back into one original equation to find the first variable․ This method is particularly effective when coefficients can be easily adjusted for elimination‚ ensuring precise solutions through systematic equation manipulation and substitution․
Using Matrices to Solve Linear Systems
Matrices provide a structured approach to solving systems of linear equations․ Begin by writing the system as an augmented matrix‚ where coefficients and constants form a rectangular array․ Use row operations to simplify the matrix into reduced row-echelon form‚ making it easy to identify solutions․ Alternatively‚ employ matrix inversion or Cramer’s Rule for systems with unique solutions․ This method is particularly efficient for larger systems and offers a systematic way to handle variables‚ ensuring accuracy and clarity in problem-solving․
Graphical Method: Finding Intersection Points
The graphical method involves plotting the equations of a system on a coordinate plane to find their intersection point‚ which represents the solution․ By graphing each equation as a line‚ the point where the lines cross identifies the values of the variables that satisfy both equations simultaneously․ This visual approach provides a clear understanding of how the equations interact and is particularly effective for systems with two variables․ However‚ accuracy depends on the scale and precision of the graph․ It is a straightforward method for simple systems but may not be practical for complex or higher-dimensional problems․

Practical Applications of Linear Systems
Linear systems are essential in business for pricing strategies‚ in engineering for optimizing designs‚ and in everyday life for budgeting and resource management‚ solving real-world problems efficiently․
Business and Economics: Pricing and Profit Scenarios
In business and economics‚ systems of linear equations are invaluable for modeling pricing strategies and maximizing profits․ By translating market dynamics into equations‚ companies can analyze how price changes affect demand and revenue․ For instance‚ setting up equations to balance costs and revenues helps determine optimal pricing points․ These systems also aid in understanding supply and demand relationships‚ enabling firms to adjust production levels and pricing strategies accordingly․ Additionally‚ linear models can forecast market trends and competitor reactions‚ ensuring informed decision-making․ This application is crucial for maintaining profitability in competitive markets and optimizing resource allocation for sustainable growth․
Engineering: Design and Optimization Problems
Engineers frequently use systems of linear equations to solve design and optimization challenges․ These equations model relationships between variables such as material strength‚ load capacities‚ and energy consumption․ For instance‚ in structural analysis‚ linear systems can determine stress distributions across beams or frameworks․ Similarly‚ in electrical engineering‚ they optimize circuit performance by balancing currents and voltages․ By translating word problems into algebraic forms‚ engineers can identify key variables and constraints‚ enabling precise calculations for design improvements․ This approach ensures efficient resource allocation‚ minimizes costs‚ and enhances overall system performance‚ making it indispensable in modern engineering practices and problem-solving․
Everyday Life: Budgeting and Resource Allocation
Linear systems are invaluable in everyday life for managing finances and allocating resources effectively․ For instance‚ creating a household budget involves setting up equations to balance income and expenses․ Variables might represent income sources‚ savings goals‚ and expenditure categories․ By translating financial scenarios into algebraic expressions‚ individuals can solve for unknowns‚ such as how much to allocate for emergencies or entertainment․ This practical application ensures efficient money management‚ helping individuals achieve financial stability and make informed decisions about resource distribution․ It simplifies complex financial planning into manageable‚ solvable equations․
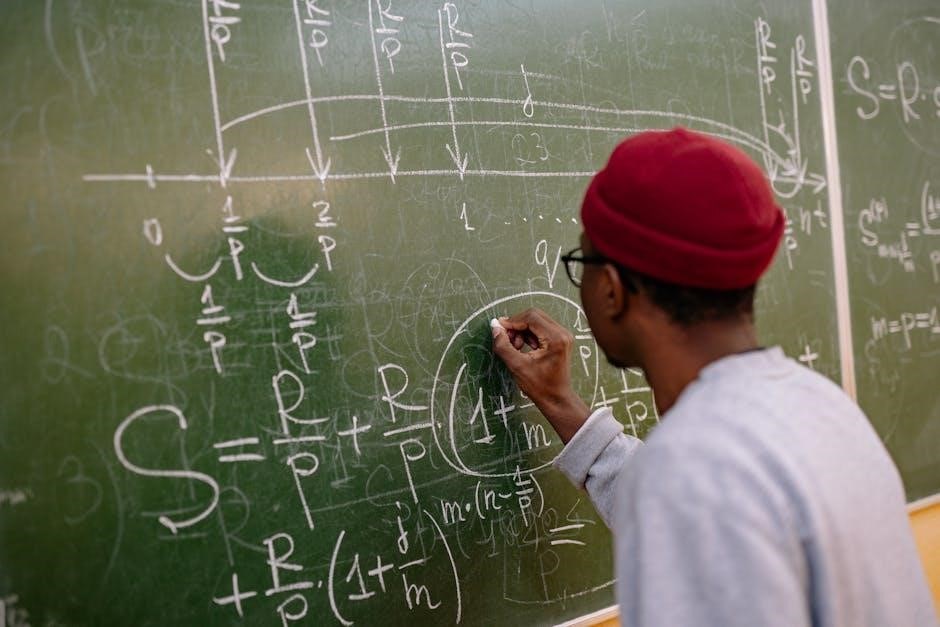
Common Word Problem Scenarios
Common word problem scenarios include mixture problems‚ work rate problems‚ and distance and speed problems‚ all of which involve translating real-life situations into systems of equations․
Mixture Problems: Combining Substances
Mixture problems involve combining substances with different properties‚ such as concentrations or costs‚ to achieve a desired result․ These problems often require setting up a system of equations to represent the total volume‚ cost‚ or concentration of the final mixture․ For example‚ mixing two solutions with different percentages of a chemical to obtain a specific concentration․ By defining variables for the quantities of each substance and translating the problem into equations‚ one can solve for the required amounts using substitution or elimination methods․ This approach ensures an accurate and efficient solution to real-world mixture scenarios․
Work Rate Problems: Time and Efficiency
Work rate problems involve determining how long it takes for individuals or machines to complete a task together or separately․ These problems often require setting up a system of equations to model the combined work rates․ For example‚ if two people can complete a job in different times individually‚ their combined work rates can be added to find the total time taken when working together․ By defining variables for their rates and total work‚ one can formulate equations to solve for the unknown time or efficiency․ This method is widely used in manufacturing and construction to optimize task completion․
Distance and Speed Problems: Motion and Travel
Distance and speed problems involve scenarios where objects or individuals are in motion‚ requiring the calculation of time‚ speed‚ or distance․ These problems often involve setting up systems of equations based on the relationship ( d = rt ) (distance equals rate multiplied by time)․ For example‚ if two vehicles are traveling toward each other‚ their combined speeds add up‚ allowing for the calculation of the time until they meet․ By defining variables for unknown quantities and translating the problem into equations‚ one can solve for the desired value‚ such as the time required to reach a destination or the speed needed to catch up․ These problems are common in travel and logistics‚ emphasizing the practical application of linear systems in real-world motion scenarios․

Advanced Techniques for Solving Word Problems
Advanced techniques involve using matrices‚ substitution‚ and elimination methods to solve complex systems efficiently․ Technology tools like graphing calculators and software also aid in visualization and verification․
Using Technology: Graphing Calculators and Software
Graphing calculators and software tools like Desmos‚ GeoGebra‚ and MATLAB simplify solving systems of linear equations․ These tools allow users to graph multiple equations simultaneously‚ visually identifying intersection points and solutions․ Advanced features enable matrix operations‚ substitution‚ and elimination methods to be performed automatically․ Additionally‚ software can solve systems symbolically‚ providing exact solutions and reducing manual calculation errors․ These technologies are invaluable for verifying solutions‚ exploring complex systems‚ and enhancing understanding of linear equation behavior․ They also support interactive learning‚ making abstract concepts more tangible for students․ Regular use of such tools fosters proficiency in solving real-world problems efficiently and accurately․
Alternative Methods: Algebraic Manipulation
Algebraic manipulation offers a systematic approach to solving systems of linear equations by rearranging terms to isolate variables or combine like terms․ Techniques include factoring‚ simplifying expressions‚ and strategically substituting known values to reduce complexity․ This method is particularly useful when standard approaches like substitution or elimination are cumbersome․ By carefully manipulating equations‚ relationships between variables become clearer‚ enabling step-by-step solutions․ These strategies enhance problem-solving flexibility and accuracy‚ especially in complex systems․ Mastery of algebraic manipulation is essential for tackling diverse word problems effectively․ It provides a foundation for advanced methods and ensures a deeper understanding of equation systems․
Tips for Verifying Solutions
Verifying solutions ensures accuracy by substituting values back into original equations․ Always check if the solution satisfies all equations in the system․ Use alternative methods like substitution or elimination to confirm results․ Graphical verification can also help by ensuring the intersection point matches the solution․ Attention to detail is crucial to avoid calculation errors․ Finally‚ interpret the solution in the context of the word problem to ensure practical relevance․ These steps enhance confidence in the solution’s validity and provide a comprehensive understanding of the system’s behavior․ Regular verification fosters Problem-solving accuracy and reliability․
Resources for Learning and Practice
Utilize PDF guides and worksheets for structured practice․ Leverage online tools and educational websites to enhance problem-solving skills and access comprehensive study materials for mastering linear systems word problems effectively․
Recommended PDF Guides and Worksheets
Enhance your learning with comprehensive PDF guides and worksheets designed to simplify systems of linear equations word problems․ These resources offer step-by-step solutions‚ practical examples‚ and exercises to improve problem-solving skills․ Many guides provide clear explanations‚ making complex concepts accessible․ Worksheets allow for hands-on practice‚ ensuring mastery of translating word problems into algebraic forms․ Popular PDFs include “Word Problems Involving Systems of Linear Equations” and “Mastering Linear Systems‚” available for free download․ These materials are ideal for students and educators seeking structured practice and deeper understanding of the subject․
Online Tools for Solving Linear Systems
Online tools like Desmos‚ Wolfram Alpha‚ and Symbolab are invaluable for solving systems of linear equations․ These platforms offer step-by-step solutions‚ graphing capabilities‚ and real-time feedback․ Desmos provides an interactive graphing calculator to visualize solutions‚ while Wolfram Alpha delivers detailed explanations․ Symbolab is user-friendly and excellent for educational purposes․ These tools are accessible online‚ making them ideal for students and professionals alike․ They can also generate solutions for word problems‚ ensuring accuracy and understanding․ Utilizing these resources can enhance problem-solving skills and provide a deeper grasp of linear systems․
Textbooks and Educational Websites
by Gilbert Strang offer comprehensive guidance on solving systems of linear equations․ Educational websites such as Khan Academy and Coursera provide interactive lessons and practice exercises․ These resources are designed to help learners master word problems by breaking down complex concepts into digestible parts․ They often include step-by-step examples‚ video tutorials‚ and quizzes to reinforce understanding․ Utilizing these textbooks and websites can significantly enhance problem-solving skills and confidence in tackling real-world applications of linear systems․
Mastery of systems of linear equations word problems enhances analytical skills‚ enabling practical applications in diverse fields like business‚ engineering‚ and everyday decision-making․
Systems of linear equations word problems involve translating real-world scenarios into mathematical models․ Key steps include identifying variables‚ converting sentences into equations‚ and solving using methods like substitution or elimination․ Graphical solutions reveal intersections‚ while matrices offer advanced techniques․ Practical applications span business‚ engineering‚ and everyday life‚ such as budgeting or resource allocation․ Common scenarios include mixture‚ work rate‚ and distance problems․ Mastery requires consistent practice and understanding of algebraic manipulation․ These problems enhance analytical skills‚ enabling students to tackle complex challenges across diverse fields effectively․ Regular practice and review of concepts are essential for long-term proficiency․
Encouragement for Further Practice
Mastery of systems of linear equations word problems is a valuable skill that enhances problem-solving abilities․ Regular practice with diverse scenarios‚ such as budgeting or engineering challenges‚ strengthens understanding․ Utilize resources like PDF guides and online tools to explore various problems․ Set goals to solve a certain number of problems weekly‚ tracking progress․ Embrace challenges as opportunities to grow․ With consistent effort‚ you’ll unlock the power of linear systems to solve real-world problems confidently and efficiently․ Keep practicing—it’s a skill that will benefit you in countless academic and professional endeavors!





